Estimates Smoothing

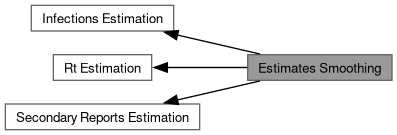
Functions for smoothing estimates using Gaussian processes. More...

Collaboration diagram for Estimates Smoothing:

Functions
vector	diagSPD_EQ (real alpha, real rho, real L, int M)
vector	diagSPD_Matern12 (real alpha, real rho, real L, int M)
vector	diagSPD_Matern32 (real alpha, real rho, real L, int M)
vector	diagSPD_Matern52 (real alpha, real rho, real L, int M)
vector	diagSPD_Periodic (real alpha, real rho, int M)
matrix	PHI (int N, int M, real L, vector x)
matrix	PHI_periodic (int N, int M, real w0, vector x)
int	setup_noise (int ot_h, int t, int horizon, int estimate_r, int stationary, int future_fixed, int fixed_from)
matrix	setup_gp (int M, real L, int dimension, int is_periodic, real w0)
void	gaussian_process_lp (vector eta)

Description

Functions for smoothing estimates using Gaussian processes.

Functions from gaussian_process.stan for implementing approximate Gaussian processes using Hilbert space methods to smooth infection and Rt trajectories.

Function Documentation

diagSPD_EQ()

vector diagSPD_EQ	(	real	alpha,
		real	rho,
		real	L,
		int	M )

These functions implement approximate Gaussian processes for Stan using Hilbert space methods. The functions are based on the following:

• https://avehtari.github.io/casestudies/Motorcycle/motorcycle_gpcourse.html (Section 4)
• https://doi.org/10.1007/s11222-022-10167-2 Spectral density for Exponentiated Quadratic kernel

Parameters

alpha	Scaling parameter
rho	Length scale parameter
L	Length of the interval
M	Number of basis functions

Returns

A vector of spectral densities

Definition at line 19 of file gaussian_process.stan.

Referenced by update_gp().

Here is the caller graph for this function:

diagSPD_Matern12()

vector diagSPD_Matern12	(	real	alpha,
		real	rho,
		real	L,
		int	M )

Spectral density for 1/2 Matern (Ornstein-Uhlenbeck) kernel

Parameters

alpha	Scaling parameter
rho	Length scale parameter
L	Length of the interval
M	Number of basis functions

Returns

A vector of spectral densities

Definition at line 37 of file gaussian_process.stan.

Referenced by update_gp().

Here is the caller graph for this function:

diagSPD_Matern32()

vector diagSPD_Matern32	(	real	alpha,
		real	rho,
		real	L,
		int	M )

Spectral density for 3/2 Matern kernel

Parameters

alpha	Scaling parameter
rho	Length scale parameter
L	Length of the interval
M	Number of basis functions

Returns

A vector of spectral densities

Definition at line 55 of file gaussian_process.stan.

Referenced by update_gp().

Here is the caller graph for this function:

diagSPD_Matern52()

vector diagSPD_Matern52	(	real	alpha,
		real	rho,
		real	L,
		int	M )

Spectral density for 5/2 Matern kernel

Parameters

alpha	Scaling parameter
rho	Length scale parameter
L	Length of the interval
M	Number of basis functions

Returns

A vector of spectral densities

Definition at line 73 of file gaussian_process.stan.

Referenced by update_gp().

Here is the caller graph for this function:

diagSPD_Periodic()

vector diagSPD_Periodic	(	real	alpha,
		real	rho,
		int	M )

Spectral density for periodic kernel

Parameters

alpha	Scaling parameter
rho	Length scale parameter
M	Number of basis functions

Returns

A vector of spectral densities

Definition at line 91 of file gaussian_process.stan.

Referenced by update_gp().

Here is the caller graph for this function:

gaussian_process_lp()

void gaussian_process_lp

(

vector

eta

)

Priors for Gaussian process (excluding length scale)

Parameters

eta	Vector of noise terms

Definition at line 226 of file gaussian_process.stan.

PHI()

matrix PHI	(	int	N,
		int	M,
		real	L,
		vector	x )

Basis functions for Gaussian Process

Parameters

N	Number of data points
M	Number of basis functions
L	Length of the interval
x	Vector of input data

Returns

A matrix of basis functions

Definition at line 112 of file gaussian_process.stan.

Referenced by setup_gp(), and update_gp().

Here is the caller graph for this function:

PHI_periodic()

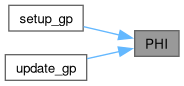
matrix PHI_periodic	(	int	N,
		int	M,
		real	w0,
		vector	x )

Basis functions for periodic Gaussian Process

Parameters

N	Number of data points
M	Number of basis functions
w0	Fundamental frequency
x	Vector of input data

Returns

A matrix of basis functions

Definition at line 132 of file gaussian_process.stan.

Referenced by setup_gp().

Here is the caller graph for this function:

setup_gp()

matrix setup_gp	(	int	M,
		real	L,
		int	dimension,
		int	is_periodic,
		real	w0 )

Setup approximate Gaussian process

Parameters

M	Number of basis functions
L	Length of the interval
dimension	Dimension of the process
is_periodic	Indicator if the process is periodic
w0	Fundamental frequency for periodic process

Returns

A matrix of basis functions

Definition at line 173 of file gaussian_process.stan.

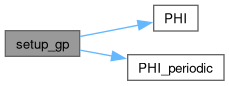
References PHI(), and PHI_periodic().

Here is the call graph for this function:

setup_noise()

int setup_noise	(	int	ot_h,
		int	t,
		int	horizon,
		int	estimate_r,
		int	stationary,
		int	future_fixed,
		int	fixed_from )

Setup Gaussian process noise dimensions

Parameters

ot_h	Observation time horizon
t	Total time points
horizon	Forecast horizon
estimate_r	Indicator if estimating r
stationary	Indicator if stationary
future_fixed	Indicator if future is fixed
fixed_from	Fixed point from

Returns

Number of noise terms

Definition at line 153 of file gaussian_process.stan.