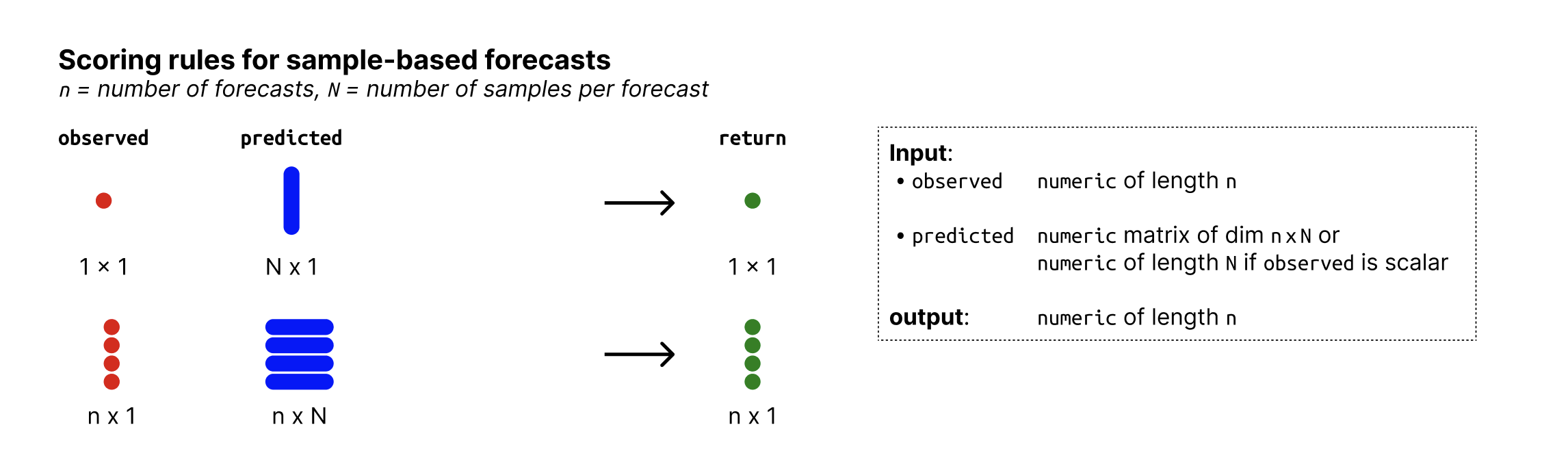
Determines bias from predictive Monte-Carlo samples. The function automatically recognises, whether forecasts are continuous or integer valued and adapts the Bias function accordingly.
Arguments
- true_values
A vector with the true observed values of size n
- predictions
nxN matrix of predictive samples, n (number of rows) being the number of data points and N (number of columns) the number of Monte Carlo samples. Alternatively, predictions can just be a vector of size n.
Details
For continuous forecasts, Bias is measured as
$$ B_t (P_t, x_t) = 1 - 2 * (P_t (x_t)) $$
where \(P_t\) is the empirical cumulative distribution function of the prediction for the true value \(x_t\). Computationally, \(P_t (x_t)\) is just calculated as the fraction of predictive samples for \(x_t\) that are smaller than \(x_t\).
For integer valued forecasts, Bias is measured as
$$ B_t (P_t, x_t) = 1 - (P_t (x_t) + P_t (x_t + 1)) $$
to adjust for the integer nature of the forecasts.
In both cases, Bias can assume values between -1 and 1 and is 0 ideally.
References
The integer valued Bias function is discussed in Assessing the performance of real-time epidemic forecasts: A case study of Ebola in the Western Area region of Sierra Leone, 2014-15 Funk S, Camacho A, Kucharski AJ, Lowe R, Eggo RM, et al. (2019) Assessing the performance of real-time epidemic forecasts: A case study of Ebola in the Western Area region of Sierra Leone, 2014-15. PLOS Computational Biology 15(2): e1006785. doi:10.1371/journal.pcbi.1006785
Author
Nikos Bosse nikosbosse@gmail.com
Examples
## integer valued forecasts
true_values <- rpois(30, lambda = 1:30)
predictions <- replicate(200, rpois(n = 30, lambda = 1:30))
bias_sample(true_values, predictions)
#> [1] -0.845 0.890 0.310 0.710 0.690 0.320 0.035 -0.600 0.605 0.790
#> [11] 0.445 -0.760 0.945 -0.210 -0.085 0.175 -0.420 0.985 0.370 -0.115
#> [21] -0.165 0.600 -0.690 -0.600 0.740 0.770 0.340 0.040 0.120 -0.880
## continuous forecasts
true_values <- rnorm(30, mean = 1:30)
predictions <- replicate(200, rnorm(30, mean = 1:30))
bias_sample(true_values, predictions)
#> [1] 0.60 -0.61 0.48 -0.70 -0.20 0.42 0.63 -0.12 -0.56 0.04 0.21 -0.38
#> [13] -0.28 -0.15 -1.00 0.01 -0.50 0.46 0.35 0.91 -0.58 -0.20 0.30 0.25
#> [25] 0.55 0.59 0.55 -0.63 0.01 -0.19