Absolute error of the median (quantile-based version)

Compute the absolute error of the median calculated as $$ \textrm{abs}(\textrm{observed} - \textrm{median prediction}) $$ The median prediction is the predicted value for which quantile_level == 0.5, the function therefore requires 0.5 to be among the quantile levels in quantile_level.

Usage

ae_median_quantile(observed, predicted, quantile_level)

Arguments

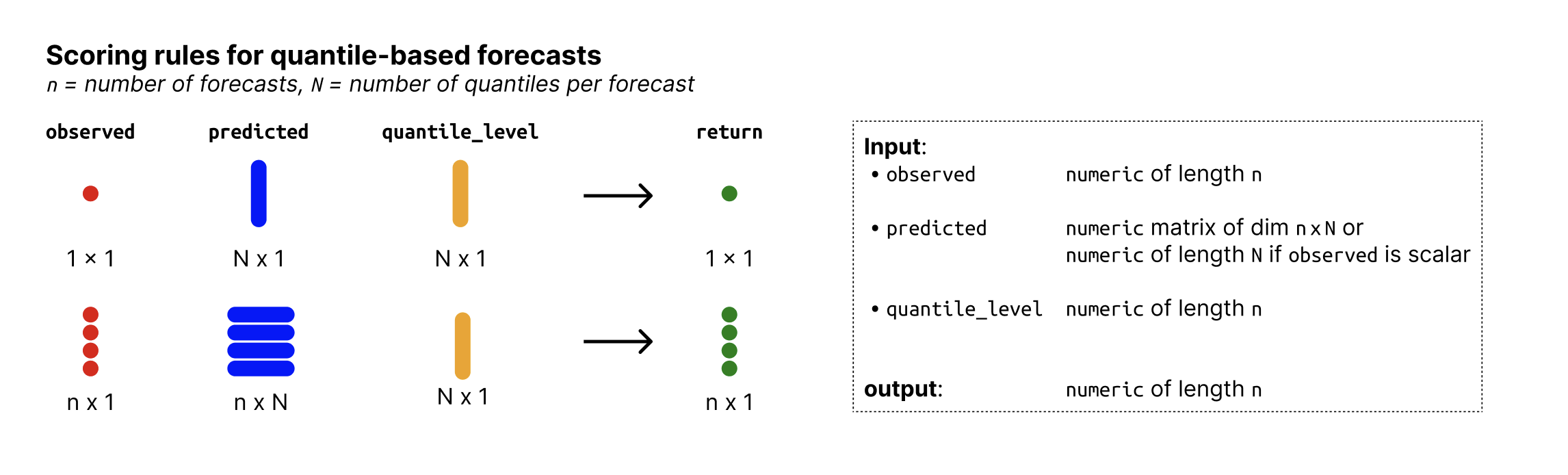
observed

Numeric vector of size n with the observed values.

predicted

Numeric nxN matrix of predictive quantiles, n (number of rows) being the number of forecasts (corresponding to the number of observed values) and N (number of columns) the number of quantiles per forecast. If observed is just a single number, then predicted can just be a vector of size N.

quantile_level

Vector of of size N with the quantile levels for which predictions were made.

Value

Numeric vector of length N with the absolute error of the median.

Input format

See also

ae_median_sample()

Examples

observed <- rnorm(30, mean = 1:30)
predicted_values <- replicate(3, rnorm(30, mean = 1:30))
ae_median_quantile(
  observed, predicted_values, quantile_level = c(0.2, 0.5, 0.8)
)
#>  [1] 2.47438940 0.92040530 3.55121603 0.24032512 1.79911603 2.12426222
#>  [7] 2.88687498 0.37899594 0.73282842 1.41674512 0.91703692 0.34483170
#> [13] 0.72770448 1.86768569 0.80586643 2.38692128 1.12876056 0.05733376
#> [19] 0.37081463 0.82374754 1.45618892 0.93544150 2.05333481 0.18155199
#> [25] 2.43676219 1.20798000 1.67648698 0.13974346 1.26067874 1.13044854