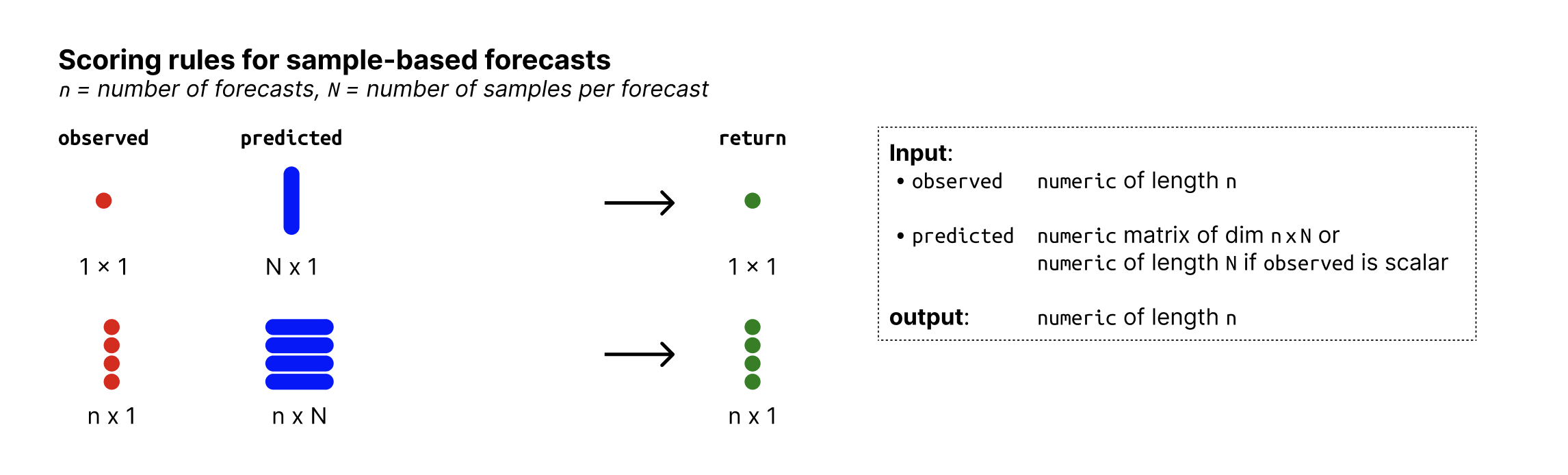
Determine bias of forecasts — bias

Determines bias from predictive Monte-Carlo samples. The function automatically recognises whether forecasts are continuous or integer valued and adapts the Bias function accordingly.

Usage

bias_sample(observed, predicted)

Arguments

observed: A vector with observed values of size n
predicted: nxN matrix of predictive samples, n (number of rows) being the number of data points and N (number of columns) the number of Monte Carlo samples. Alternatively, predicted can just be a vector of size n.

Value

Numeric vector of length n with the biases of the predictive samples with respect to the observed values.

Details

For continuous forecasts, Bias is measured as

$$ B_t (P_t, x_t) = 1 - 2 * (P_t (x_t)) $$

where $P_t$ is the empirical cumulative distribution function of the prediction for the observed value $x_t$. Computationally, $P_t (x_t)$ is just calculated as the fraction of predictive samples for $x_t$ that are smaller than $x_t$.

For integer valued forecasts, Bias is measured as

$$ B_t (P_t, x_t) = 1 - (P_t (x_t) + P_t (x_t + 1)) $$

to adjust for the integer nature of the forecasts.

In both cases, Bias can assume values between -1 and 1 and is 0 ideally.

Input format

Overview of required input format for sample-based forecasts

References

The integer valued Bias function is discussed in Assessing the performance of real-time epidemic forecasts: A case study of Ebola in the Western Area region of Sierra Leone, 2014-15 Funk S, Camacho A, Kucharski AJ, Lowe R, Eggo RM, et al. (2019) Assessing the performance of real-time epidemic forecasts: A case study of Ebola in the Western Area region of Sierra Leone, 2014-15. PLOS Computational Biology 15(2): e1006785. doi:10.1371/journal.pcbi.1006785

Examples


## integer valued forecasts
observed <- rpois(30, lambda = 1:30)
predicted <- replicate(200, rpois(n = 30, lambda = 1:30))
bias_sample(observed, predicted)
#>  [1] -0.650 -0.135 -0.805 -0.660  0.425  0.995  0.440 -0.935  0.525 -0.630
#> [11] -0.965 -0.625 -0.735 -0.470  0.420 -0.720  0.275  0.380 -0.675  0.480
#> [21]  0.165  0.840  0.755  0.035  0.160 -0.860  0.025  0.460 -0.405  0.915

## continuous forecasts
observed <- rnorm(30, mean = 1:30)
predicted <- replicate(200, rnorm(30, mean = 1:30))
bias_sample(observed, predicted)
#>  [1] -0.46  0.02  0.02  0.12 -0.18 -0.07  0.96 -0.60  0.16 -0.31  0.79  0.49
#> [13] -0.74 -0.48  0.26 -0.56  0.82  0.89  0.41 -0.31  0.19  0.47 -0.85  0.32
#> [25]  0.15 -0.16  0.34 -0.30  0.80  0.27