Interval coverage (for quantile-based forecasts)

Check whether the observed value is within a given central prediction interval. The prediction interval is defined by a lower and an upper bound formed by a pair of predictive quantiles. For example, a 50% prediction interval is formed by the 0.25 and 0.75 quantiles of the predictive distribution.

Usage

interval_coverage(observed, predicted, quantile_level, interval_range = 50)

Arguments

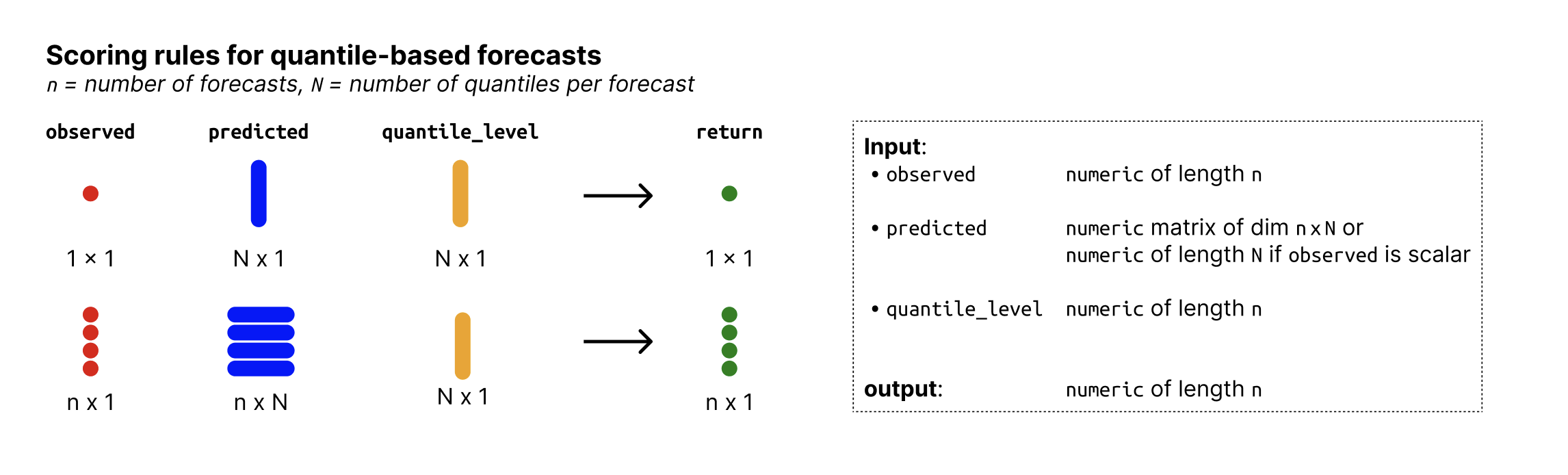
observed

Numeric vector of size n with the observed values.

predicted

Numeric nxN matrix of predictive quantiles, n (number of rows) being the number of forecasts (corresponding to the number of observed values) and N (number of columns) the number of quantiles per forecast. If observed is just a single number, then predicted can just be a vector of size N.

quantile_level

Vector of of size N with the quantile levels for which predictions were made.

interval_range

A single number with the range of the prediction interval in percent (e.g. 50 for a 50% prediction interval) for which you want to compute interval coverage.

Value

A vector of length n with elements either TRUE, if the observed value is within the corresponding prediction interval, and FALSE otherwise.

Input format

Overview of required input format for quantile-based forecasts

Examples

observed <- c(1, -15, 22)
predicted <- rbind(
  c(-1, 0, 1, 2, 3),
  c(-2, 1, 2, 2, 4),
   c(-2, 0, 3, 3, 4)
)
quantile_level <- c(0.1, 0.25, 0.5, 0.75, 0.9)
interval_coverage(observed, predicted, quantile_level)
#> [1]  TRUE FALSE FALSE