Quantile score — quantile_score • scoringutils

Proper Scoring Rule to score quantile predictions. Smaller values are better. The quantile score is closely related to the interval score (see wis()) and is the quantile equivalent that works with single quantiles instead of central prediction intervals.

The quantile score, also called pinball loss, for a single quantile level $\tau$ is defined as $$ \text{QS}_\tau(F, y) = 2 \cdot \{ \mathbf{1}(y \leq q_\tau) - \tau\} \cdot (q_\tau - y) = \begin{cases} 2 \cdot (1 - \tau) * q_\tau - y, & \text{if } y \leq q_\tau\\ 2 \cdot \tau * |q_\tau - y|, & \text{if } y > q_\tau, \end{cases} $$ with $q_\tau$ being the $\tau$-quantile of the predictive distribution $F$, and $\mathbf{1}(\cdot)$ the indicator function.

The weighted interval score for a single prediction interval can be obtained as the average of the quantile scores for the lower and upper quantile of that prediction interval: $$ \text{WIS}_\alpha(F, y) = \frac{\text{QS}_{\alpha/2}(F, y) + \text{QS}_{1 - \alpha/2}(F, y)}{2}. $$ See the SI of Bracher et al. (2021) for more details.

quantile_score() returns the average quantile score across the quantile levels provided. For a set of quantile levels that form pairwise central prediction intervals, the quantile score is equivalent to the interval score.

Usage

quantile_score(observed, predicted, quantile_level, weigh = TRUE)

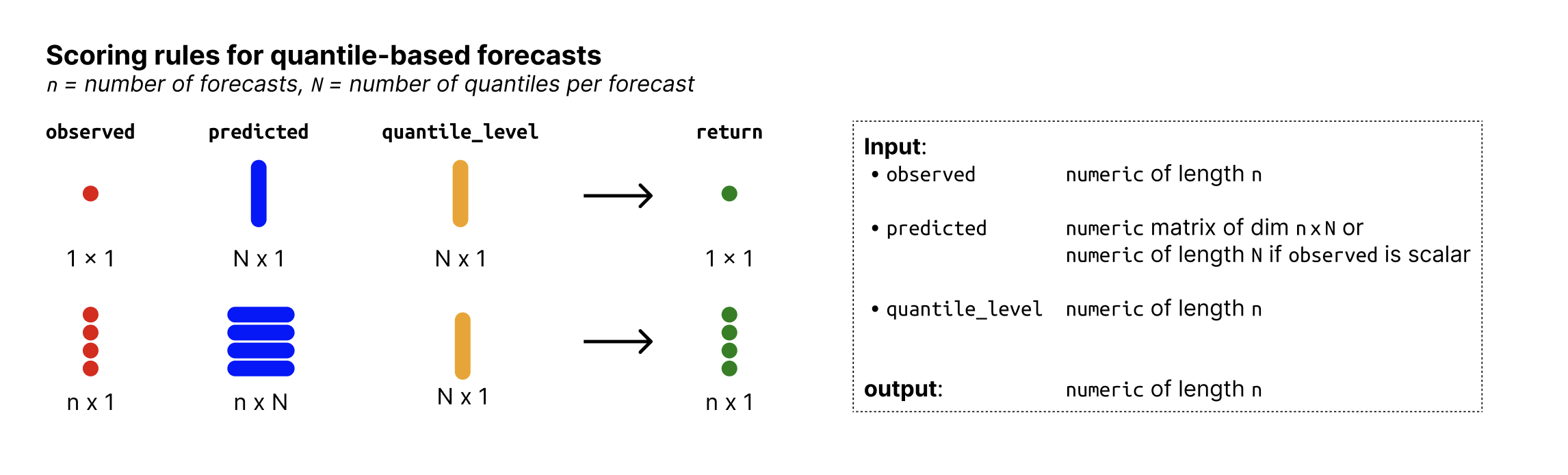
Arguments

observed: Numeric vector of size n with the observed values.
predicted: Numeric nxN matrix of predictive quantiles, n (number of rows) being the number of forecasts (corresponding to the number of observed values) and N (number of columns) the number of quantiles per forecast. If observed is just a single number, then predicted can just be a vector of size N.
quantile_level: Vector of of size N with the quantile levels for which predictions were made.
weigh: Logical. If TRUE (the default), weigh the score by $\alpha / 2$, so it can be averaged into an interval score that, in the limit (for an increasing number of equally spaced quantiles/prediction intervals), corresponds to the CRPS. $\alpha$ is the value that corresponds to the ($\alpha/2$) or ($1 - \alpha/2$), i.e. it is the decimal value that represents how much is outside a central prediction interval (E.g. for a 90 percent central prediction interval, alpha is 0.1).

Value

Numeric vector of length n with the quantile score. The scores are averaged across quantile levels if multiple quantile levels are provided (the result of calling rowMeans() on the matrix of quantile scores that is computed based on the observed and predicted values).

Input format

Overview of required input format for quantile-based forecasts

References

Strictly Proper Scoring Rules, Prediction,and Estimation, Tilmann Gneiting and Adrian E. Raftery, 2007, Journal of the American Statistical Association, Volume 102, 2007 - Issue 477

Evaluating epidemic forecasts in an interval format, Johannes Bracher, Evan L. Ray, Tilmann Gneiting and Nicholas G. Reich, 2021, https://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1008618

Examples

observed <- rnorm(10, mean = 1:10)
alpha <- 0.5

lower <- qnorm(alpha / 2, observed)
upper <- qnorm((1 - alpha / 2), observed)

qs_lower <- quantile_score(observed,
  predicted = matrix(lower),
  quantile_level = alpha / 2
)
qs_upper <- quantile_score(observed,
  predicted = matrix(upper),
  quantile_level = 1 - alpha / 2
)
interval_score <- (qs_lower + qs_upper) / 2
interval_score2 <- quantile_score(
  observed,
  predicted = cbind(lower, upper),
  quantile_level = c(alpha / 2, 1 - alpha / 2)
)

# this is the same as the following
wis(
  observed,
  predicted = cbind(lower, upper),
  quantile_level = c(alpha / 2, 1 - alpha / 2)
)
#>  [1] 0.3372449 0.3372449 0.3372449 0.3372449 0.3372449 0.3372449 0.3372449
#>  [8] 0.3372449 0.3372449 0.3372449