Weighted interval score (WIS) — wis • scoringutils

The WIS is a proper scoring rule used to evaluate forecasts in an interval- / quantile-based format. See Bracher et al. (2021). Smaller values are better.

As the name suggest the score assumes that a forecast comes in the form of one or multiple central prediction intervals. A prediction interval is characterised by a lower and an upper bound formed by a pair of predictive quantiles. For example, a 50% central prediction interval is formed by the 0.25 and 0.75 quantiles of the predictive distribution.

Interval score

The interval score (IS) is the sum of three components: overprediction, underprediction and dispersion. For a single prediction interval only one of the components is non-zero. If for a single prediction interval the observed value is below the lower bound, then the interval score is equal to the absolute difference between the lower bound and the observed value ("underprediction"). "Overprediction" is defined analogously. If the observed value falls within the bounds of the prediction interval, then the interval score is equal to the width of the prediction interval, i.e. the difference between the upper and lower bound. For a single interval, we therefore have:

$$ \textrm{IS} = (\textrm{upper} - \textrm{lower}) + \frac{2}{\alpha}(\textrm{lower} - \textrm{observed}) * \mathbf{1}(\textrm{observed} < \textrm{lower}) + \frac{2}{\alpha}(\textrm{observed} - \textrm{upper}) * \mathbf{1}(\textrm{observed} > \textrm{upper}) $$ where $\mathbf{1}()$ is the indicator function and indicates how much is outside the prediction interval. $\alpha$ is the decimal value that indicates how much is outside the prediction interval. For a 90% prediction interval, for example, $\alpha$ is equal to 0.1. No specific distribution is assumed, but the interval formed by the quantiles has to be symmetric around the median (i.e you can't use the 0.1 quantile as the lower bound and the 0.7 quantile as the upper bound). Non-symmetric quantiles can be scored using the function quantile_score().

For a set of $k = 1, \dots, K$ prediction intervals and the median $m$, we can compute a weighted interval score (WIS) as the sum of the interval scores for individual intervals: $$ \text{WIS}_{\alpha_{\{0:K\}}}(F, y) = \frac{1}{K + 1/2} \times \left(w_0 \times |y - m| + \sum_{k=1}^{K} \left\{ w_k \times \text{IS}_{\alpha_k}(F, y) \right\}\right) $$

The individual scores are usually weighted with $w_k = \frac{\alpha_k}{2}$. This weight ensures that for an increasing number of equally spaced quantiles, the WIS converges to the continuous ranked probability score (CRPS).

Quantile score

In addition to the interval score, there also exists a quantile score (QS) (see quantile_score()), which is equal to the so-called pinball loss. The quantile score can be computed for a single quantile (whereas the interval score requires two quantiles that form an interval). However, the intuitive decomposition into overprediction, underprediction and dispersion does not exist for the quantile score.

Two versions of the weighted interval score

There are two ways to conceptualise the weighted interval score across several quantiles / prediction intervals and the median.

In one view, you would treat the WIS as the average of quantile scores (and the median as 0.5-quantile) (this is the default for wis()). In another view, you would treat the WIS as the average of several interval scores + the difference between the observed value and median forecast. The effect of that is that in contrast to the first view, the median has twice as much weight (because it is weighted like a prediction interval, rather than like a single quantile). Both are valid ways to conceptualise the WIS and you can control the behaviour with the count_median_twice-argument.

WIS components: WIS components can be computed individually using the functions overprediction, underprediction, and dispersion.

Usage

wis(
  observed,
  predicted,
  quantile_level,
  separate_results = FALSE,
  weigh = TRUE,
  count_median_twice = FALSE,
  na.rm = FALSE
)

dispersion_quantile(observed, predicted, quantile_level, ...)

overprediction_quantile(observed, predicted, quantile_level, ...)

underprediction_quantile(observed, predicted, quantile_level, ...)

Arguments

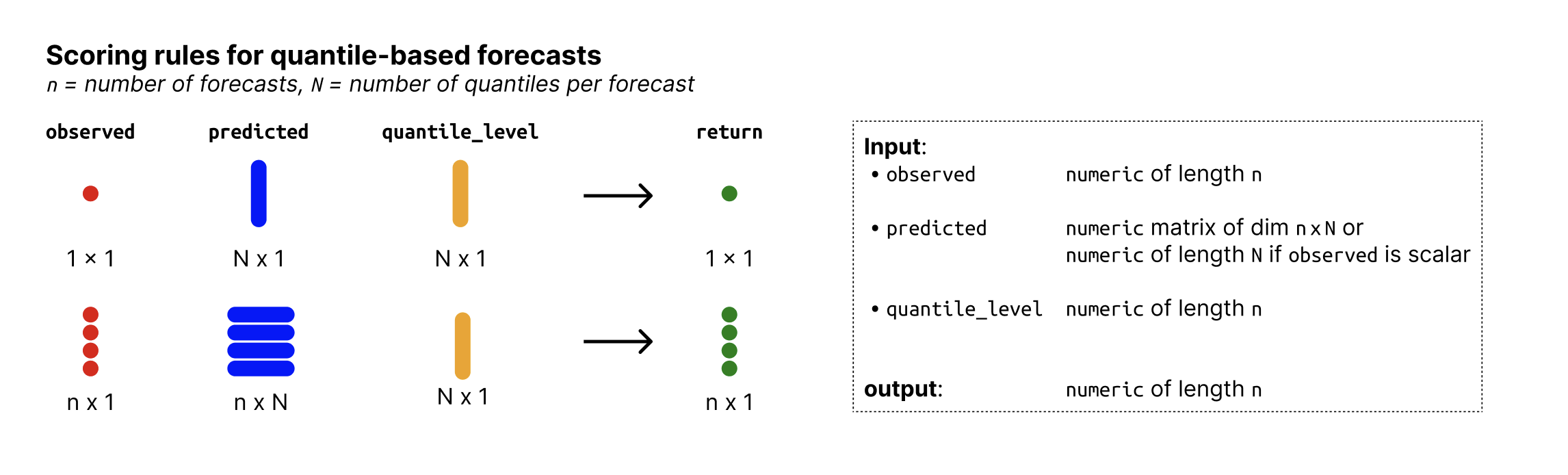
observed: Numeric vector of size n with the observed values.
predicted: Numeric nxN matrix of predictive quantiles, n (number of rows) being the number of forecasts (corresponding to the number of observed values) and N (number of columns) the number of quantiles per forecast. If observed is just a single number, then predicted can just be a vector of size N.
quantile_level: Vector of of size N with the quantile levels for which predictions were made.
separate_results: Logical. If TRUE (default is FALSE), then the separate parts of the interval score (dispersion penalty, penalties for over- and under-prediction get returned as separate elements of a list). If you want a data.frame instead, simply call as.data.frame() on the output.
weigh: Logical. If TRUE (the default), weigh the score by $\alpha / 2$, so it can be averaged into an interval score that, in the limit (for an increasing number of equally spaced quantiles/prediction intervals), corresponds to the CRPS. $\alpha$ is the value that corresponds to the ($\alpha/2$) or ($1 - \alpha/2$), i.e. it is the decimal value that represents how much is outside a central prediction interval (E.g. for a 90 percent central prediction interval, alpha is 0.1).
count_median_twice: If TRUE, count the median twice in the score.
na.rm: If TRUE, ignore NA values when computing the score.
...: Additional arguments passed on to wis() from functions overprediction_quantile(), underprediction_quantile() and dispersion_quantile().

Value

wis(): a numeric vector with WIS values of size n (one per observation), or a list with separate entries if separate_results is TRUE.

dispersion_quantile(): a numeric vector with dispersion values (one per observation).

overprediction_quantile(): a numeric vector with overprediction values (one per observation).

underprediction_quantile(): a numeric vector with underprediction values (one per observation)

Input format

Overview of required input format for quantile-based forecasts

References

Evaluating epidemic forecasts in an interval format, Johannes Bracher, Evan L. Ray, Tilmann Gneiting and Nicholas G. Reich, 2021, https://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1008618

Examples

observed <- c(1, -15, 22)
predicted <- rbind(
  c(-1, 0, 1, 2, 3),
  c(-2, 1, 2, 2, 4),
  c(-2, 0, 3, 3, 4)
)
quantile_level <- c(0.1, 0.25, 0.5, 0.75, 0.9)
wis(observed, predicted, quantile_level)
#> [1]  0.36 15.34 19.14